3 The method
Given a kernel \(w_h(t)\) with bandwidth \(h\), we will be considering the following EM-inspired algorithm.
Here’s a high-level look at the algorithm. We’ll discuss the initialization, E-step, and M-step in the next subsections.
#' A Kernel-smoothed EM algorithm that fits a mixture of Gaussians that evolves over time. The larger any of the three bandwidths are, the smoother the corresponding parameter will vary.
#'
#' Element t in the list `y`, `y[[t]]`, is an n_t-by-d matrix with the coordinates of every point (or bin) at time t given in each row. `biomass[[t]]` is a numeric vector of length n_t, where the ith entry of the vector is the biomass for the bin whose coordinates are given in the ith row of `y[[t]]`.
#'
#' The initial_fit parameter is a list of initial parameter values that is generated from the initialization functions in the package. It contains initial values at all times for mu, Sigma, and pi, as well as estimates for the responsibilities and cluster membership. Currently, for our cluster membership estimates (z estimate - zest), each bin is assigned to the cluster that is most responsible for it.
#'
<<y-param>>
#' @param K number of clusters/populations
#' @param hmu bandwidth for mu parameter
#' @param hSigma bandwidth for Sigma parameter
#' @param hpi bandwidth for pi parameter
#' @param dates A vector of POSIXct (or POSIXt) date-time objects of length T, where each element represents the timestamp corresponding to the t-th observation. If provided, these dates are converted to numeric values and rescaled (by dividing by 3600) for time-based smoothing operations. If omitted, the function defaults to using the sequence of observation indices.
#' @param num_iter number of iterations of EM to perform
#' @param biomass list of length T, where each element `biomass[[t]]` is a
#' numeric vector of length n_t containing the biomass (or count) of particles
#' in each bin
#' @param initial_fit a list of starting values for the parameters, responsibilities, and estimated cluster assignments
#' @export
kernel_em <- function (y, K, hmu, hSigma, hpi, dates = NULL, num_iter = 10,
biomass = default_biomass(y),
initial_fit = init_const(y, K, 50, 50)) {
num_times <- length(y)
d <- ncol(y[[1]])
mu <- initial_fit$mu
Sigma <- initial_fit$Sigma
pi <- initial_fit$pi
if (!is.null(dates)){
numeric_dates <- as.numeric(dates)
rescaled_dates <- (numeric_dates - min(numeric_dates)) / 3600
}
for (l in seq(num_iter)) {
<<E-step>>
<<M-step>>
}
zest <- resp %>% purrr::map(~ max.col(.x))
dimnames(mu) <- list(NULL, paste0("cluster", 1:K), NULL)
dimnames(Sigma) <- list(NULL, paste0("cluster", 1:K), NULL, NULL)
dimnames(pi) <- list(NULL, paste0("cluster", 1:K))
list(mu = mu, Sigma = Sigma, pi = pi, resp = resp, zest = zest)
}To start off our first E-step, we need estimates of \((\mu,\Sigma,\pi)\) for every cluster for every time point, which we get from our initialization. Before diving into the initialization, however, let us first look at the main algorithm:
3.1 E-step
Given an estimate of \((\mu,\Sigma,\pi)\), the E-step computes for each \(Y_{it}\) how “responsible” each cluster is for it. In particular, the responsibility vector \((\hat\gamma_{it1},\ldots,\hat\gamma_{itK})\) is a probability vector. It is computed using Bayes rule:
\[ \hat\gamma_{itk}=\hat{\mathbb{P}}(Z_{it}=k|Y_{it})=\frac{\hat \pi_{tk}\phi(Y_{it};\hat\mu_{tk},\hat\Sigma_{tk})}{\sum_{\ell=1}^K\hat \pi_{t\ell}\phi(Y_{it};\hat\mu_{t\ell },\hat\Sigma_{t\ell})} \]
We will create a function that calculates responsibilities given parameter estimates, as we will need to calculate responsibilities elsewhere too (in the initialization). In the function below, we calculate responsibilities using the log of the densities to help with numerical stability, and we use matrixStats::rowLogSumExps(), which implements the LogSumExp function (also called RealSoftMax) in a stable way.
#' Calculates responsibilities for each point (or bin) at each time point, given parameter estimates for all clusters at all times
<<y-param>>
#' @param mu a T-by-K-by-d array of means
#' @param Sigma a T-K-by-d-by-d array of covariance matrices
#' @param pi a T-by-K vector of probabilities
#' @export
calculate_responsibilities <- function(y, mu, Sigma, pi){
resp <- list() # responsibilities gamma[[t]][i, k]
log_resp <- list() # log of responsibilities
d <- ncol(y[[1]])
K <- ncol(mu)
num_times <- length(y)
if (d == 1) {
for (tt in seq(num_times)) {
log_phi <- matrix(NA, nrow(y[[tt]]), K)
for (k in seq(K)) {
log_phi[, k] <- stats::dnorm(y[[tt]],
mean = mu[tt, k, 1],
sd = sqrt(Sigma[tt, k, 1, 1]), log = TRUE)
}
log_temp = t(t(log_phi) + log(pi[tt, ]))
log_resp[[tt]] = log_temp - matrixStats::rowLogSumExps(log_temp)
resp[[tt]] = exp(log_resp[[tt]])
}
} else if (d > 1) {
for (tt in seq(num_times)) {
log_phi <- matrix(NA, nrow(y[[tt]]), K)
for (k in seq(K)) {
log_phi[, k] <- mvtnorm::dmvnorm(y[[tt]],
mean = mu[tt, k, ],
sigma = Sigma[tt, k, , ], log = TRUE)
}
log_temp = t(t(log_phi) + log(pi[tt, ]))
log_resp[[tt]] = log_temp - matrixStats::rowLogSumExps(log_temp)
resp[[tt]] = exp(log_resp[[tt]])
}
}
return(resp)
}3.2 M-step
In the M-step, we update the estimates of \((\mu,\Sigma,\pi)\):
We now assume that we are working with binned data, where \(C_i^{(t)}\) is the number of particles (or the biomass) at time \(t\) in bin \(i\), where \(i\) goes from \(1\) to \(B\), the total number of bins. In the case of unbinned data, we take \(C_i^{(t)} = 1\) for each point in the data. \[ \hat\gamma_{\cdot sk}=\sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}, \] which is an estimate of the number of points (or total biomass) in class \(k\) at time \(s\), and define
\[ \tilde\gamma_{\cdot tk}=\sum_{s=1}^Tw_{h_\pi}(t-s)\hat\gamma_{\cdot sk}, \] which is a smoothed version of this estimate.
Then we estimate \(\pi\) as follows:
\[ \hat\pi_{tk}=\frac{\sum_{s=1}^Tw_{h_\pi}(t-s)\hat\gamma_{\cdot sk}}{\sum_{s=1}^T{w_{h_\pi}(t-s)n_s}}=\frac{\tilde\gamma_{\cdot tk}}{\sum_{s=1}^T{w_{h_\pi}(t-s)n_s}} \] where \(n_s = \sum_{i=1}^{B} C_i^{(s)}\) is the total number of points (or total biomass) at time \(s\).
For \(\mu\):
\[ \hat\mu_{tk}=\frac{\sum_{s=1}^Tw_{h_\mu}(t-s)\sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}Y_{is}}{\sum_{s=1}^Tw_{h_\mu}(t-s)\hat\gamma_{\cdot sk}} \]
For \(\Sigma\):
\[ \hat\Sigma_{tk}=\frac{\sum_{s=1}^Tw_{h_\Sigma}(t-s)\sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}(Y_{is}-\hat\mu_{sk})(Y_{is}-\hat\mu_{sk})^\top}{\sum_{s=1}^Tw_{h_\Sigma}(t-s)\hat\gamma_{\cdot sk}} \]
Each of these quantities involves a summation over \(i\) before the smoothing over time. In each case we do the summation over \(i\) first so that then all quantities can be expressed as an array (rather than as lists). This should make the smoothing more efficient.
3.2.1 M-step \(\pi\)
For \(\pi\) estimation, we compute
\[ \hat\gamma_{\cdot sk}=\sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}, \] And then we compute the kernel smoothed version of this:
\[ \tilde\gamma_{\cdot tk}=\sum_{s=1}^Tw_{h_\pi}(t-s)\hat\gamma_{\cdot sk}, \]
We are then ready to compute the following:
\[ \hat\pi_{tk}=\frac{\sum_{s=1}^Tw_{h_\pi}(t-s)\hat\gamma_{\cdot sk}}{\sum_{s=1}^T{w_{h_\pi}(t-s)n_s}}=\frac{\tilde\gamma_{\cdot tk}}{\sum_{s=1}^T{w_{h_\pi}(t-s)n_s}} \]
Here is an example that demonstrates how the ksmooth() function works:
xx <- 5 * sin((1:100) / 5) + rnorm(100)
plot(xx, type="o")
lines(stats::ksmooth(1:length(xx), xx, bandwidth = 5, x.points = 1:length(xx)), col="red")
lines(stats::ksmooth(1:length(xx), xx, bandwidth = 20, x.points = 1:length(xx)), col="blue")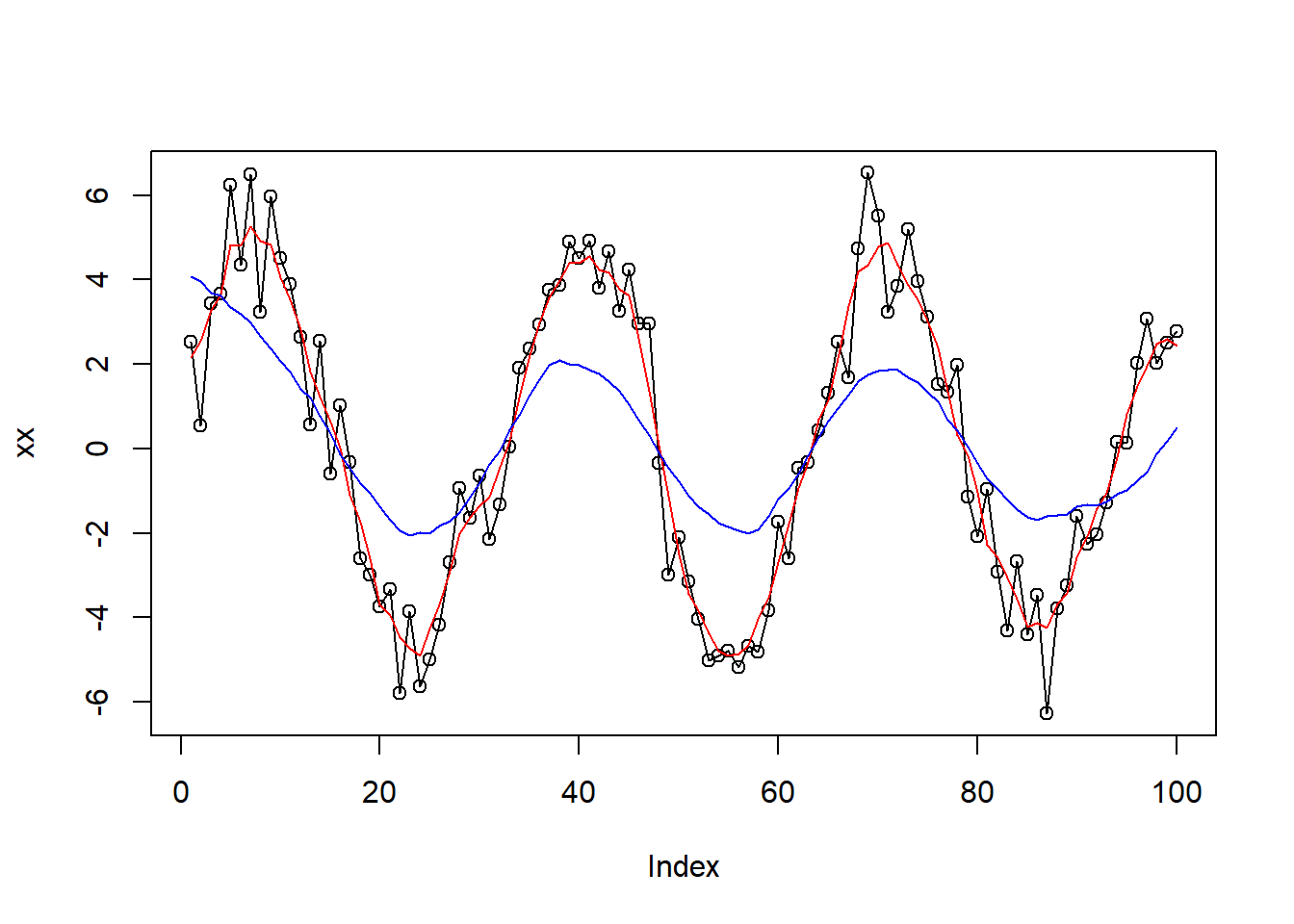
3.2.2 M-step \(\mu\)
Next, we compute the estimate of \(\mu\). We again first compute the unsmoothed estimate and then apply smoothing to it:
\[ \sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}Y_{is} \] This is then used in the following smoothed estimate:
\[ \hat\mu_{tk}=\frac{\sum_{s=1}^Tw_{h_\mu}(t-s)\sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}Y_{is}}{\sum_{s=1}^Tw_{h_\mu}(t-s)\hat\gamma_{\cdot sk}} \]
In the above code for y_sum, I convert a list of length \(T\), where each list element is a \(K\times d\) matrix, to a \(T\times K\times d\) array. To verify that this conversion is done correctly, I tried this small example:
## [[1]]
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 11
## [4,] 4 8 12
##
## [[2]]
## [,1] [,2] [,3]
## [1,] 13 17 21
## [2,] 14 18 22
## [3,] 15 19 23
## [4,] 16 20 24## , , 1
##
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 11
## [4,] 4 8 12
##
## , , 2
##
## [,1] [,2] [,3]
## [1,] 13 17 21
## [2,] 14 18 22
## [3,] 15 19 23
## [4,] 16 20 243.2.3 M-step \(\Sigma\)
We start by computing
\[ \sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}(Y_{is}-\hat\mu_{sk})(Y_{is}-\hat\mu_{sk})^\top \]
and then go on to compute
\[ \hat\Sigma_{tk}=\frac{\sum_{s=1}^Tw_{h_\Sigma}(t-s)\sum_{i=1}^{B}C_i^{(s)}\hat\gamma_{isk}(Y_{is}-\hat\mu_{sk})(Y_{is}-\hat\mu_{sk})^\top}{\sum_{s=1}^Tw_{h_\Sigma}(t-s)\hat\gamma_{\cdot sk}} \]
3.3 Initialization
First, we begin with a function that creates a “default biomass” for data that is unbinned (we give each point a biomass (or count) of 1).
#' Creates a biomass list of length T, where each element `biomass[[t]]` is a numeric vector of length n_t containing just 1's.
<<y-param>>
#' @export
default_biomass <- function(y) {
biomasslist <- vector("list", length(y))
for (i in 1:length(y)) {
biomasslist[[i]] <- as.numeric(rep(1, dim(y[[i]])[1]))
}
return(biomasslist)
}We have tried numerous ways of initializing: randomly sampling points for a constant initialization, fitting a separate mixture model to each time point and trying to match clusters using the Hungarian algorithm, having a “chain of EM-algorithms”, with each one initialized by the previous time; and using a Bayesian approach, which is described below. The methods we settled on are the constant initialization and the Bayesian initialization. The kernel-EM algorithm seems to be able to do about the same with both initializations, and so even though the Bayesian approach gives better results, the speed of the constant initialization makes it the practical choice.
3.3.1 Constant Initialization
We get a constant initialization by randomly sampling time points, and then from each sampled time point, randomly sampling some points, and fitting a regular EM-algorithm using the mclust package to the randomly chosen points.
#' Initialize the Kernel EM-algorithm using constant parameters
#'
<<y-param>>
#' @param K number of components
#' @param times_to_sample number of time points to sample
#' @param points_to_sample number of bins to sample from each sampled time point
#' @export
init_const <- function (y, K, times_to_sample = 50, points_to_sample = 50){
num_times <- length(y)
d <- ncol(y[[1]])
mu <- array(NA, c(num_times, K, d))
Sigma <- array(NA, c(num_times, K, d, d))
pi <- matrix(NA, num_times, K)
# Repeatedly call Mclust until it gives a non-NULL fit:
init_fit <- NULL
while (is.null(init_fit)) {
# subsample data:
sampled_times <- sample(num_times, times_to_sample, replace=TRUE)
if (d == 1) {
sample_data <- y[sampled_times] %>%
purrr::map(~ .x[sample(nrow(.x), points_to_sample, replace=TRUE)]) %>%
unlist()
}
else {
sample_data <- y[sampled_times] %>%
purrr::map(~ t(.x[sample(nrow(.x), points_to_sample, replace=TRUE), ])) %>%
unlist() %>%
matrix(ncol = d, byrow = TRUE)
}
if (d == 1) {
init_fit <- mclust::Mclust(sample_data, G = K, modelNames = "V")
for (tt in seq(num_times)) {
mu[tt, , 1] <- init_fit$parameters$mean
Sigma[tt, , 1, 1] <- init_fit$parameters$variance$sigmasq
pi[tt, ] <- init_fit$parameters$pro
}
} else if (d > 1) {
init_fit <- mclust::Mclust(sample_data, G = K, modelNames = "VVV")
if (is.matrix(init_fit$parameters$mean)){
for (tt in seq(num_times)) {
mu[tt, ,] <- t(init_fit$parameters$mean)
pi[tt, ] <- init_fit$parameters$pro
Sigma[tt, , , ] <- aperm(init_fit$parameters$variance$sigma, c(3,1,2))
}
}
}
}
#calculate responsibilities
resp <- calculate_responsibilities(y, mu, Sigma, pi)
zest <- resp %>% purrr::map(~ max.col(.x))
list(mu = mu, Sigma = Sigma, pi = pi, resp = resp, zest = zest)
}In the above, we concatenated a list of matrices. Here’s a small example to verify that this is working as intended:
list_of_mats <- list(matrix(1:10, 2, 5), matrix(11:25, 3, 5))
list_of_mats
list(list_of_mats) %>%
purrr::map(~ t(.x)) %>%
unlist() %>%
matrix(ncol = 5, byrow = TRUE)## [[1]]
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 3 5 7 9
## [2,] 2 4 6 8 10
##
## [[2]]
## [,1] [,2] [,3] [,4] [,5]
## [1,] 11 14 17 20 23
## [2,] 12 15 18 21 24
## [3,] 13 16 19 22 25## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 2 3 4 5
## [2,] 6 7 8 9 10
## [3,] 11 12 13 14 15
## [4,] 16 17 18 19 20
## [5,] 21 22 23 24 25Let’s have a look at what the initialization does on our example data.
ex1_init_const = init_const(ex1$dat$y, K = 2)
plot_data_and_model(ex1$dat$y, ex1_init_const$zest, ex1_init_const$mu)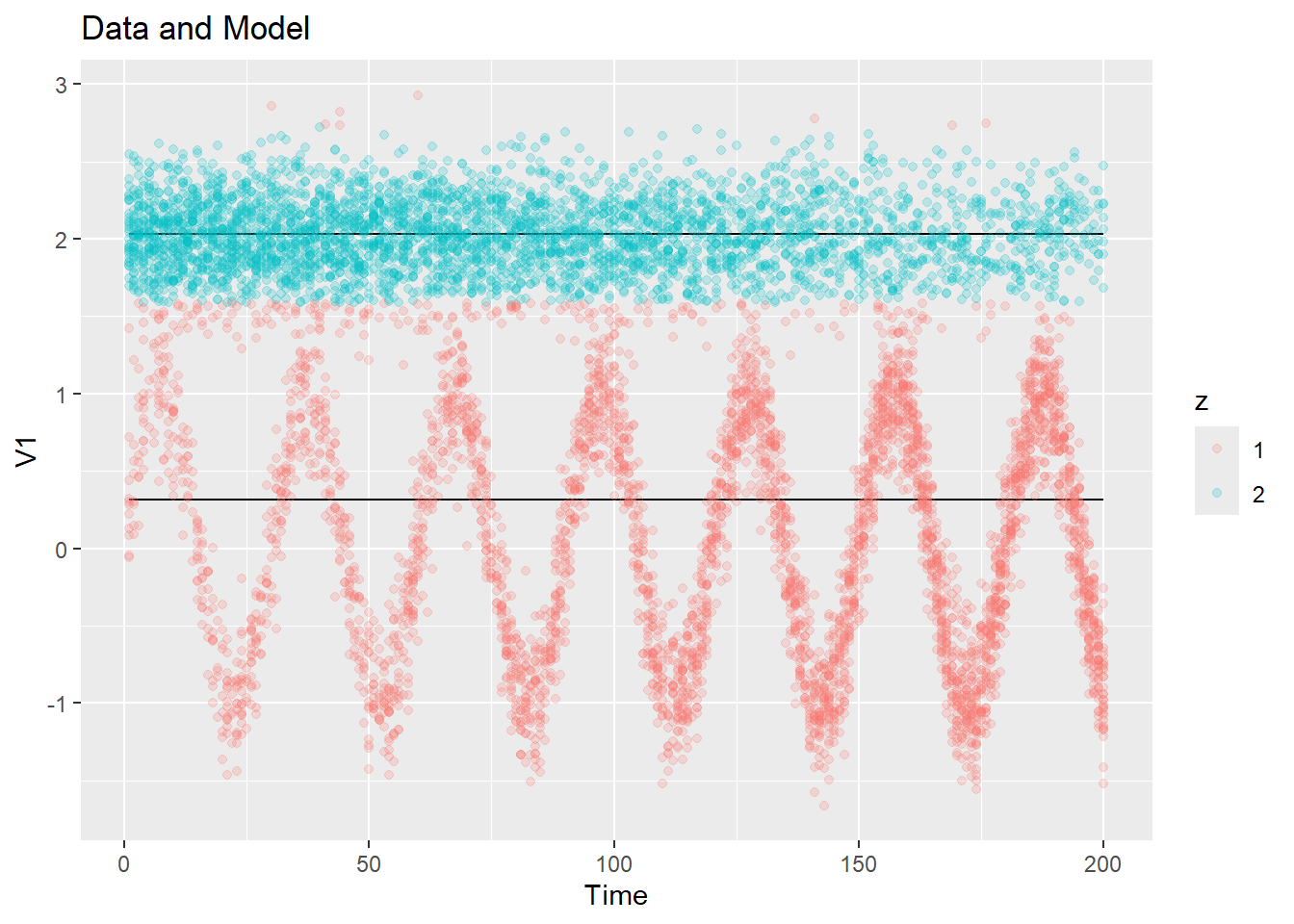
What about the 3-d initialization?
ex2_init_const = init_const(ex2$dat$y, K = 4)
plot_data_and_model(ex2$dat$y, ex2_init_const$zest, ex2_init_const$mu)Pretty reasonable centers were chosen! If we get a bad initialization by chance (an unlucky random sampling), we can always re-run the constant initialization as it is very cheap.
3.3.2 Bayesian Initialization
We’d like to have an initialization method that can vary with time yet can do well even for time points where there is only a small number of particles in a given cluster. The idea is to take a Bayesian approach in which the previous time point serves as the prior for the next time point. The implicit assumption is that the parameters vary sufficiently smoothly that the previous time point’s parameter values are a reasonable estimate of the next time point’s parameter values. For now, we take the priors to be based on the previous time point, but we can also consider priors formed based on all previous time points.
Let \(\tilde\gamma_{itk} = C_i^{(t)}\gamma_{itk}\), which are “weighted responsibilities”, where each \(\gamma_{itk}\) has been multiplied with the corresponding biomass of bin \(i\) at time \(t\). We use these weighted responsibilities in our Bayesian approach (can make it unweighted to simplify).
3.3.2.1 M-step \(\pi\)
For \(\pi_{tk}\), we assume a Dirichlet prior, getting a posterior mean of: (this specific calculation needs to be double checked)
At time \(t\) we imagine estimating the number of points in each class \(k\), which is
\[ n_t\hat{\pi}_{tk}|\pi_{tk}\sim\text{Multinomial}(n_t,\pi_{t}) \]
where \(\hat{\pi}_{tk},\pi_{tk}\) are \(K\)-dimensional probability vectors. Our prior takes the previous number of points
\[ \pi_{tk}\sim \text{Dirichlet}(n_{t-1}\hat{\pi}_{t-1k}). \]
(Here we are conditioning on everything that happened before time \(t\), but omitting this in the notation.)
Thus, the posterior is
\[ \pi_{tk}|n_t\hat\pi_{tk}\sim \text{Dirichlet}(n_t\hat\pi_{tk}+n_{t-1}\hat{\pi}_{t-1}) \]
and the posterior mean is thus
\[ \mathbb{E}[\pi_{tk}|n_t\hat\pi_{tk}]=\frac{n_t\hat\pi_{tk}+n_{t-1}\hat{\pi}_{t-1,k}}{\sum_{k=1}^K[n_t\hat\pi_{tk}+n_{t-1}\hat{\pi}_{t-1,k}]}=\frac{n_t\hat\pi_{tk}+n_{t-1}\hat{\pi}_{t-1,k}}{n_t+n_{t-1}}. \]
In other words, we estimate the vector \(\pi_{tk}\) to be the convex combination \(\alpha_t\hat\pi_{tk}+(1-\alpha_t)\hat\pi_{t-1k}\), where \(\alpha_t=n_t/(n_t+n_{t-1})\). Our final estimate is therefore
\[ \hat{\pi}_{tk} = \frac{\left(\sum_{i=1}^{n_t} \tilde\gamma_{itk}\right) + \left(\sum_{i=1}^{n_{t-1}} \tilde\gamma_{it-1k}\right)} {n_{t-1} + n_{t}} \]
where \(n_t = \sum_{i=1}^{B} C_i^{(t)}\) is the total number of points (or total biomass) at time \(t\). Here, \(B\) is the total number of bins (or points, if the data is unbinned).
3.3.2.2 M-step \(\mu\)
For estimating \(\mu_{tk}\), we assume that we known covariance matrix at time \(t\): \(\hat\Sigma_{t-1,k}\) (the previous time’s estimate); and we assume a multivariate normal prior centered around the previous time’s mean, with the scaled covariance matrix:
\[ \mu_{tk}\sim\mathcal{N}(\hat{\mu}_{t-1,k}, \frac{1}{n_{t-1,k}} \hat\Sigma_{t-1,k}) \]
We then get the following posterior: \[ \mu_{tk}|\hat{\mu}_{tk}\sim\mathcal{N}(\frac{n_{tk}\bar{Y}_{it} + n_{t-1}\hat{\mu}_{t-1,k}}{n_{tk}+n_{t-1,k}}, \frac{1}{n_{t-1,k} + n_{tk}} \hat\Sigma_{t-1,k}) \]
where \(\bar{Y}_{it} = \frac{\sum_{i=1}^{n_{t}} \tilde\gamma_{itk}Y_{it}}{\sum_{i=1}^{n_{t}} \tilde\gamma_{itk}}\) can be thought of as the mean of our data points in cluster \(k\) at time \(t\). Our estimate for \(\mu_{tk}\) is then \[ \hat{\mu}_{tk} = \mathbb{E}[\mu_{tk}|\hat\mu_{tk}] = \frac{ \sum_{i=1}^{n_t} \tilde\gamma_{itk} Y_{it} + \left(\sum_{i=1}^{n_{t-1}} \tilde\gamma_{i,t-1,k}\right) \hat{\mu}_{t-1,k}} { \left(\sum_{i=1}^{n_t} \tilde\gamma_{itk}\right) + \left(\sum_{i=1}^{n_{t-1}} \tilde\gamma_{i,t-1,k}\right)} \]
3.3.2.3 M-step \(\Sigma\)
We then estimate \(\hat\Sigma_{tk}\) in a similar way, assuming a prior that’s an inverse-Wishart with mean \(\hat\Sigma_{t-1,k}\). Our estimate is:
\[ \hat{\Sigma}_{tk} = \frac{\left(\sum_{i=1}^{n_{t-1}} \tilde\gamma_{i,t-1,k}\right) \Sigma_{k,t-1} + \sum_{i=1}^{n_t} \tilde\gamma_{itk} \left(Y_{it} - \mu_{tk}\right) \left(Y_{it} - \mu_{tk}\right)^T} {\left(\sum_{i=1}^{n_{t-1}} \tilde\gamma_{i,t-1,k}\right) + \left(\sum_{i=1}^{n_t} \tilde\gamma_{itk}\right)} \]
A bit more thought is required regarding what multiple iterations (default number of iterations is 1) of this Bayesian EM-algorithm would do (on the second iteration and above, we use \(\mu_{kt}\) from the previous iteration in the place of \(\mu_{t-1,k}\), and similarly for \(\Sigma_{tk}\) and \(\pi_{tk}\)).
We also add the option to introduce Laplace smoothing for calculating the responsibilities, to prevent \(\pi_{tk}\) collapsing to 0 over time for some clusters. The Laplace smoothing works by replacing the responsibilities calculation with:
\[ \hat\gamma_{itk}=\hat{\mathbb{P}}(Z_{it}=k|Y_{it})=\frac{\hat \pi_{tk}\phi(Y_{it};\hat\mu_{tk},\hat\Sigma_{tk}) + \alpha \min_{c} \hat \pi_{tc}\phi(Y_{it};\hat\mu_{tc},\hat\Sigma_{tc})}{\sum_{\ell=1}^K \left( \hat \pi_{t\ell}\phi(Y_{it};\hat\mu_{t\ell },\hat\Sigma_{t\ell}) + \alpha \min_{c} \hat \pi_{tc}\phi(Y_{it};\hat\mu_{tc},\hat\Sigma_{tc}) \right)} \]
where \(\alpha_L\) is the Laplace smoothing constant (which defaults to 0). Here is the function that implements this approach:
#' Initialize the Kernel EM-algorithm using Bayesian methods
#'
<<y-param>>
#' @param K number of components
#' @param biomass list of length T, where each element `biomass[[t]]` is a
#' numeric vector of length n_t containing the biomass (or count) of particles
#' in each bin
#' @param num_iter number of iterations of EM to perform #need to think more
#' about iterations for Bayes init
#' @param lap_smooth_const Laplace smoothing constant #More explanation needed
#' @export
init_bayes <- function (y, K, biomass = default_biomass(y), num_iter = 1,
lap_smooth_const = 0){
num_times <- length(y)
d <- ncol(y[[1]])
resp <- list() # responsibilities gamma[[t]][i, k]
log_resp <- list()
resp_weighted <- list()
resp_sum <- list()
resp_sum_pi <- list()
y_sum <- list()
mat_sum <- list()
yy <- list()
mu <- array(NA, c(num_times, K, d))
Sigma <- array(NA, c(num_times, K, d, d))
pi <- matrix(NA, num_times, K)
if (d == 1){
init_fit <- mclust::Mclust(y[[1]], G = K, modelNames = "V")
ii = 1
while (is.null(init_fit) == TRUE){
init_fit <- mclust::Mclust(y[[1 + ii]], G = K, modelNames = "V")
ii = ii + 1
}
mu[1, , 1] <- init_fit$parameters$mean
Sigma[1, , 1, 1] <- init_fit$parameters$variance$sigmasq
pi [1, ] <- init_fit$parameters$pro
} else if (d > 1){
init_fit <- mclust::Mclust(y[[1]], G = K, modelNames = "VVV")
ii = 1
while (is.null(init_fit) == TRUE){
init_fit <- mclust::Mclust(y[[1 + ii]], G = K, modelNames = "V")
ii = ii + 1
}
mu[1, ,] <- t(init_fit$parameters$mean)
pi[1, ] <- init_fit$parameters$pro
Sigma[1, , , ] <- aperm(init_fit$parameters$variance$sigma, c(3,1,2))
}
phi <- matrix(NA, nrow(y[[1]]), K)
log_phi <- matrix(NA, nrow(y[[1]]), K)
if (d == 1) {
for (k in seq(K)) {
log_phi[, k] <- stats::dnorm(y[[1]],
mean = mu[1, k, 1],
sd = sqrt(Sigma[1, k, 1, 1]), log = TRUE)
}
} else if (d > 1) {
for (k in seq(K)) {
log_phi[, k] <- mvtnorm::dmvnorm(y[[1]],
mean = mu[1, k, ],
sigma = Sigma[1, k, , ], log = TRUE)
}
}
log_temp = t(t(log_phi) + log(pi[1, ]))
log_resp = log_temp - matrixStats::rowLogSumExps(log_temp)
resp[[1]] = exp(log_resp)
resp_weighted[[1]] = diag(biomass[[1]]) %*% resp[[1]]
resp_sum[[1]] <- colSums(resp_weighted[[1]]) %>%
unlist() %>%
matrix(ncol = K, byrow = TRUE)
pi_prev <- pi
mu_prev <- mu
Sigma_prev <- Sigma
for (tt in 2:num_times){
for (l in seq(num_iter)) {
# E-step
phi <- matrix(NA, nrow(y[[tt]]), K)
if (l == 1){
if (d == 1) {
for (k in seq(K)) {
phi[, k] <- stats::dnorm(y[[tt]],
mean = mu_prev[tt - 1, k, 1],
sd = sqrt(Sigma_prev[tt - 1, k, 1, 1]))
}
} else if (d > 1) {
for (k in seq(K)) {
phi[, k] <- mvtnorm::dmvnorm(y[[tt]],
mean = mu_prev[tt - 1, k, ],
sigma = Sigma_prev[tt - 1, k, , ])
}
}
temp <- t(t(phi) * pi_prev[tt - 1, ])
}else if (l > 1) {
if (d == 1) {
for (k in seq(K)) {
phi[, k] <- stats::dnorm(y[[tt]],
mean = mu_prev[tt, k, 1],
sd = sqrt(Sigma_prev[tt, k, 1, 1]))
}
} else if (d > 1) {
for (k in seq(K)) {
phi[, k] <- mvtnorm::dmvnorm(y[[tt]],
mean = mu_prev[tt, k, ],
sigma = Sigma_prev[tt, k, , ])
}
}
temp <- t(t(phi) * pi_prev[tt, ])
}
temp_smooth = temp + lap_smooth_const * apply(temp, 1, min)
resp[[tt]] <- temp_smooth / rowSums(temp_smooth)
resp_weighted[[tt]] = diag(biomass[[tt]]) %*% resp[[tt]]
zest <- resp %>% purrr::map(~ max.col(.x))
#M-step
#M-step pi
resp_sum[[tt]] <- colSums(resp_weighted[[tt]]) %>%
unlist() %>%
matrix(ncol = K, byrow = TRUE)
for (k in seq(K)){
pi[tt, k] <- (resp_sum [[tt - 1]][, k] + resp_sum [[tt]][, k]) / (rowSums(resp_sum[[tt - 1]]) + rowSums(resp_sum[[tt]]))
}
#M-step mu
y_sum[[tt]] <- crossprod(resp_weighted[[tt]], y[[tt]]) %>%
unlist() %>%
array(c(K, d))
for (k in seq(K)){
mu[tt, k, ] <- ((resp_sum[[tt - 1]][, k] * mu[tt - 1, k , ]) + y_sum[[tt]][k, ]) / (resp_sum[[tt - 1]][, k] + resp_sum[[tt]][, k])
}
#M-step Sigma
mat_sum[[tt]] <- array(NA, c(K, d, d))
yy[[tt]] <- matrix(NA, dim(y[[tt]])[1], d)
for (k in seq(K)) {
for(dd in seq(d)) {
yy [[tt]][, dd] <- (y[[tt]][, dd]- mu[tt, k, dd])
}
mat_sum[[tt]][k, , ] <- crossprod(yy[[tt]], yy[[tt]] * resp_weighted[[tt]][, k]) # YY^T * D * YY
}
for (k in seq(K)){
Sigma[tt, k, , ] <- ((resp_sum[[tt - 1]][, k] * Sigma[tt - 1, k, , ]) + mat_sum[[tt]][k, , ]) / (resp_sum[[tt - 1]] [, k] + resp_sum[[tt]] [, k])
}
pi_prev <- pi
mu_prev <- mu
Sigma_prev <- Sigma
}
}
dimnames(mu) <- list(NULL, paste0("cluster", 1:K), NULL)
dimnames(Sigma) <- list(NULL, paste0("cluster", 1:K), NULL, NULL)
dimnames(pi) <- list(NULL, paste0("cluster", 1:K))
zest <- resp %>% purrr::map(~ max.col(.x))
fit_init = list(mu = mu, Sigma = Sigma, pi = pi, resp = resp, zest = zest)
return(fit_init)
}Here is what the Bayes initialization gives for the same example data:
ex1_init_bayes = init_bayes(ex1$dat$y, K = 2)
plot_data_and_model(ex1$dat$y, ex1_init_bayes$zest, ex1_init_bayes$mu)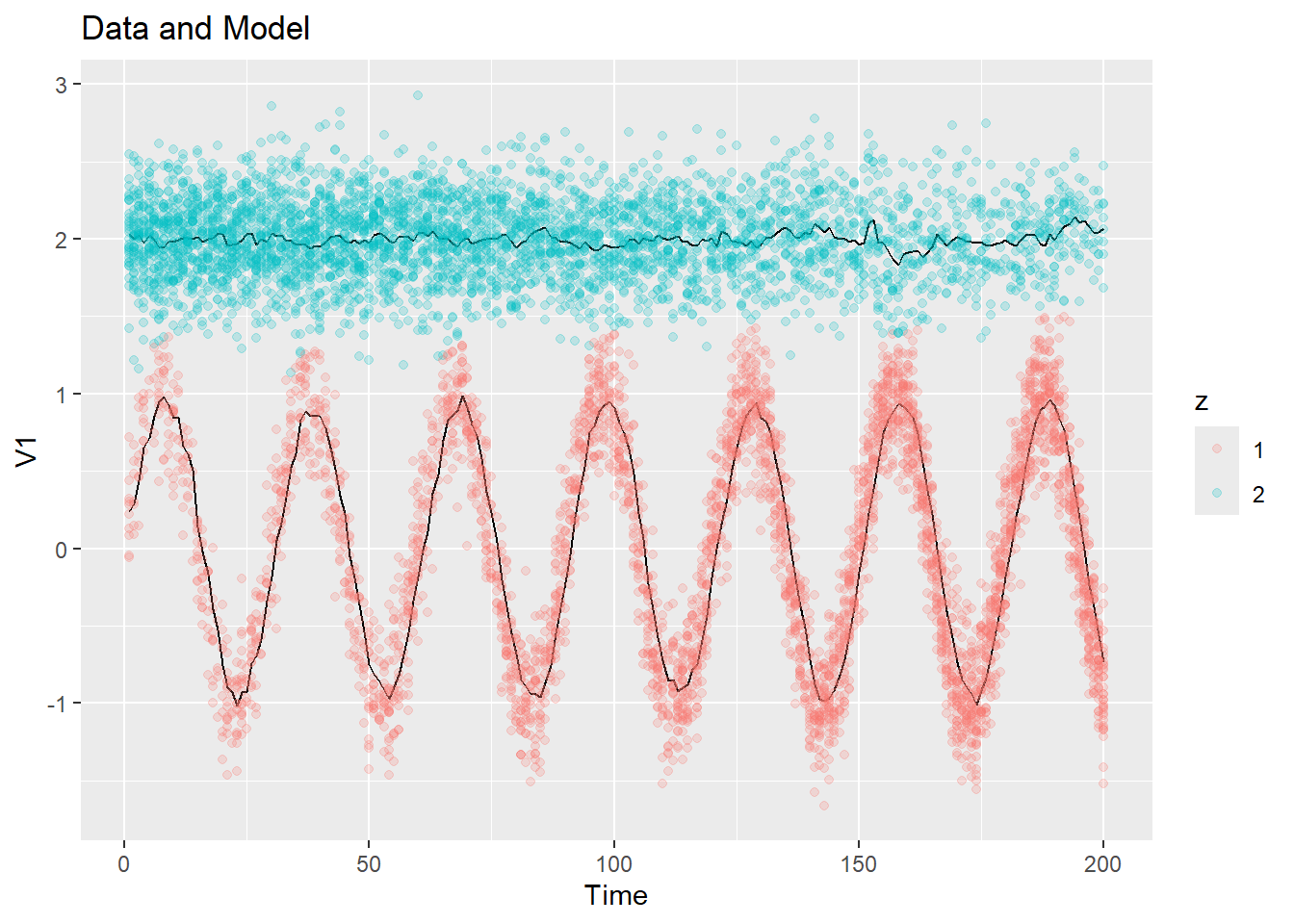
This is much better than the constant initialization! But it will be significantly more computationally expensive with real data.
Here is the 3-d example:
ex2_init_bayes = init_bayes(ex2$dat$y, K = 4)
plot_data_and_model(ex2$dat$y, ex2_init_bayes$zest, ex2_init_bayes$mu)Let’s add the necessary packages to our package:
## ✔ Adding 'mclust' to Imports field in DESCRIPTION
## • Refer to functions with `mclust::fun()`## ✔ Adding 'matrixStats' to Imports field in DESCRIPTION
## • Refer to functions with `matrixStats::fun()`Now that we have responsibilities, we can plot the biomass for each cluster over time:
plot_biomass(ex2$dat$biomass, ex2_init_bayes$resp)The lines are so jagged because we independently drew from a normal distribution for the biomass of each “bin” at each time.
3.4 Trying out the method
Let’s first try out our 1-d example, with all bandwidths equal to 5. Notice that no initialization is explicitly fed into the kernel_em() function, so it will use a constant initialization.
fit <- kernel_em(ex1$dat$y, K = 2, hmu = 5, hSigma = 5, hpi = 5, num_iter = 20)
plot_data_and_model(ex1$dat$y, fit$zest, fit$mu)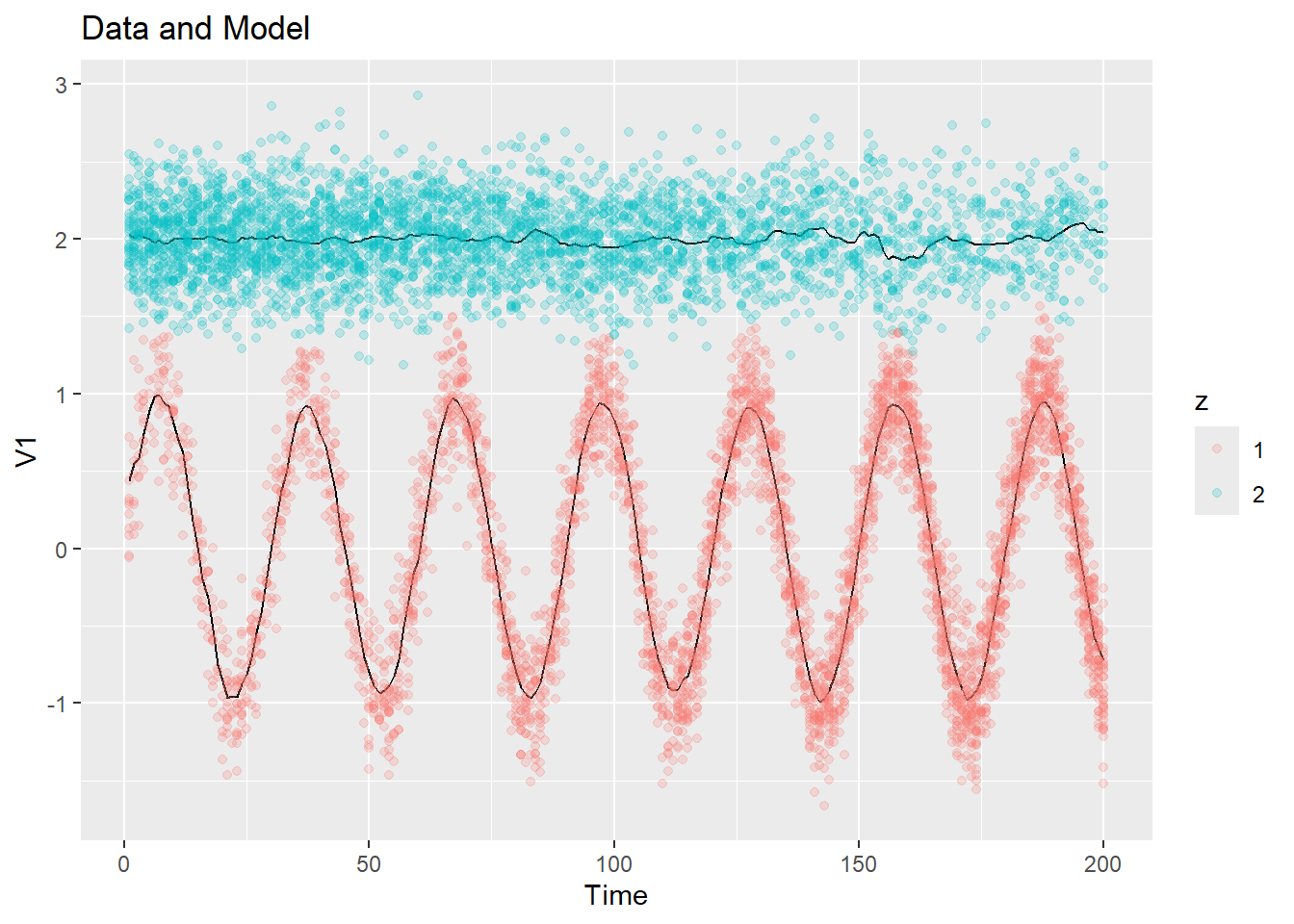
Now let’s try bandwidths equal to 50.
fit <- kernel_em(ex1$dat$y, K = 2, hmu = 50, hSigma = 50, hpi = 50, num_iter = 10, initial_fit = ex1_init_const)
plot_data_and_model(ex1$dat$y, fit$zest, fit$mu)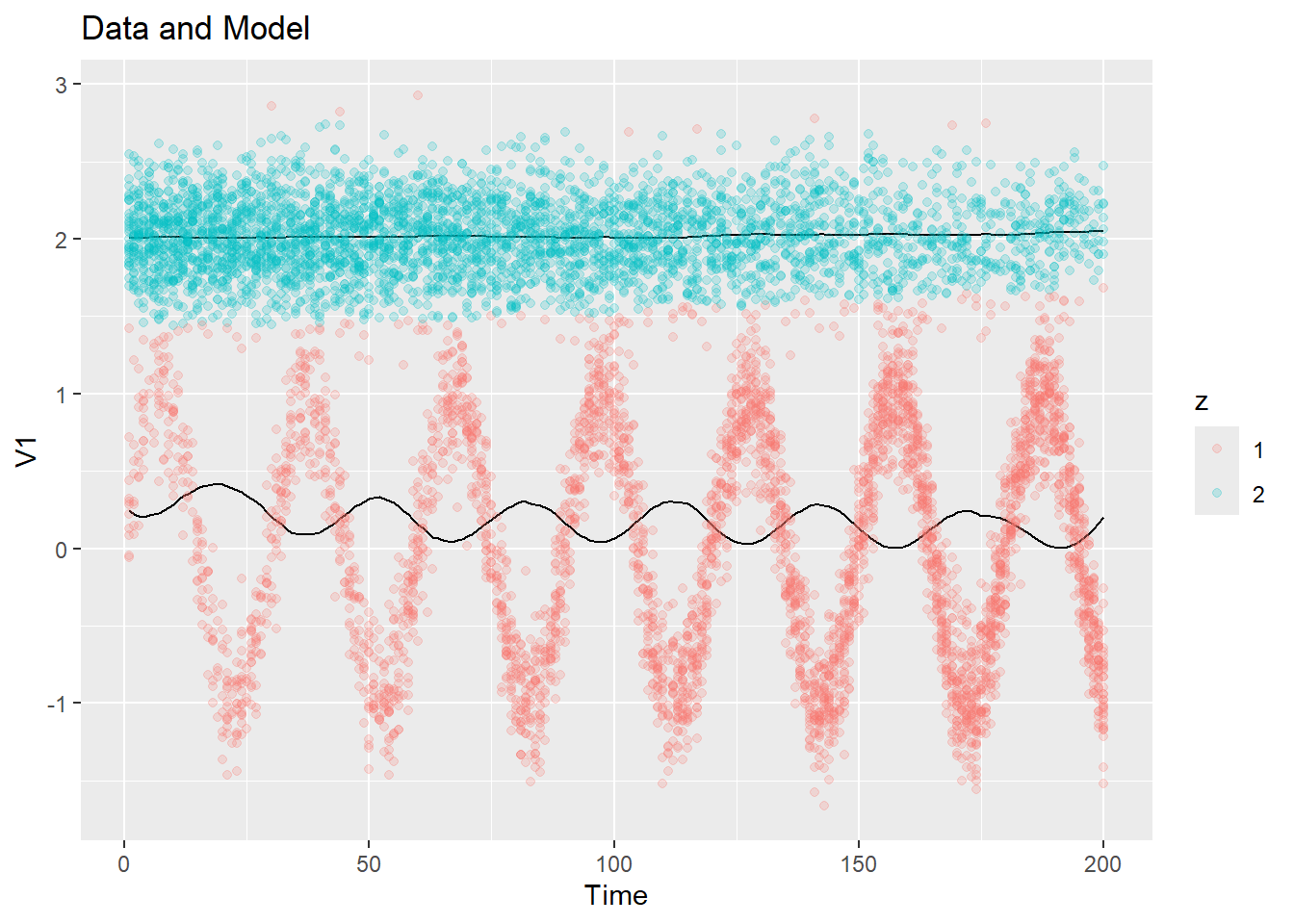
Now let’s try out our 3-d example, with bandwidths 5 again:
fit <- kernel_em(ex2$dat$y, K = 4, hmu = 5, hSigma = 5, hpi = 5, num_iter = 10, initial_fit = ex2_init_const)
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu)Let’s look at how the \(\pi\)’s and \(\mu\)’s evolve over time:
plot_pi(fit$pi)
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu, dim = 1, show_data = FALSE)We can look at how the means evolve in any dimension with the data too:
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu, dim = 2)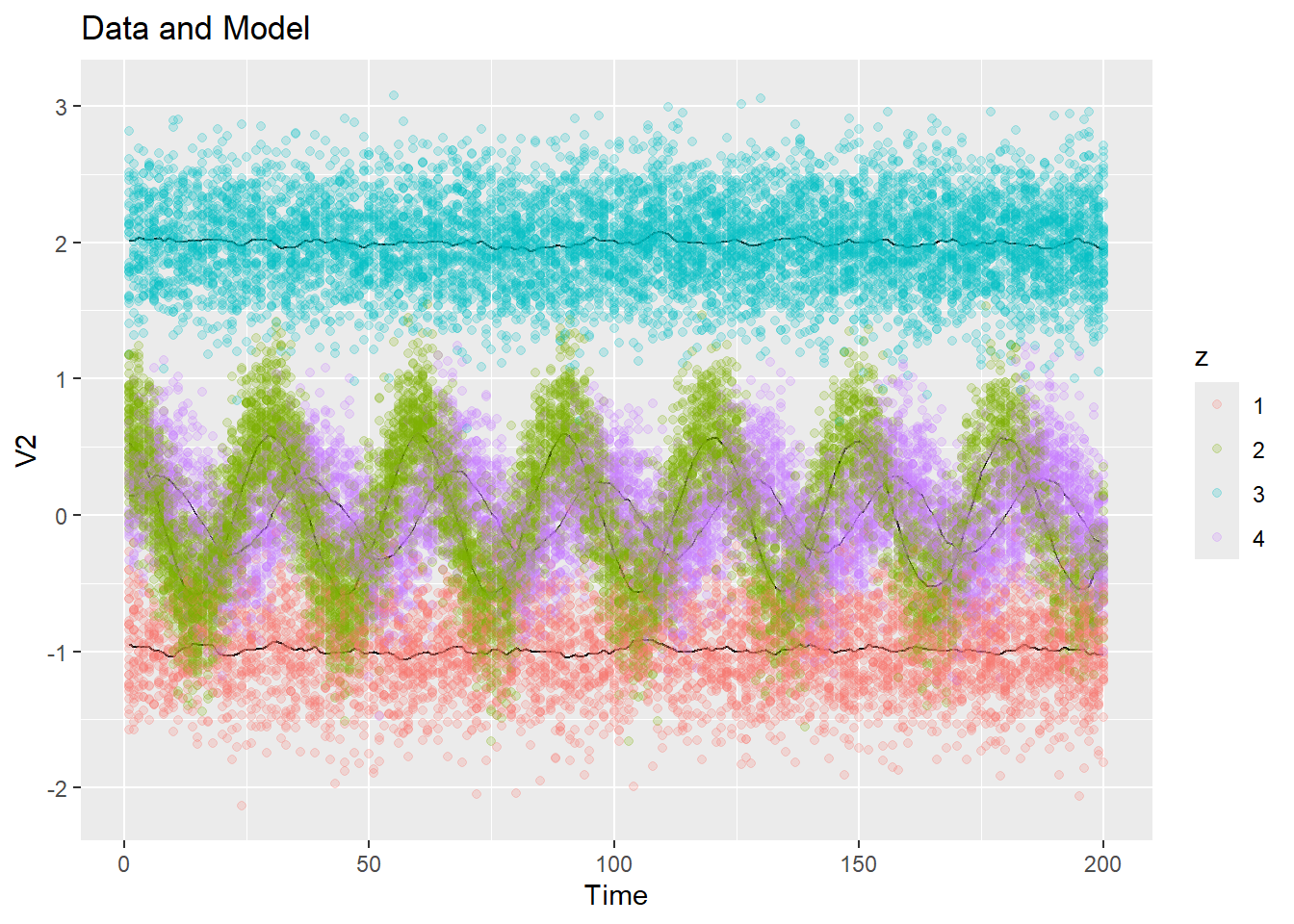
Let’s have a look at the responsibilities that we get from our model. We consider the first 4 bins in the 50th time point:
## [,1] [,2] [,3] [,4]
## [1,] 2.844005e-24 1.283566e-16 2.284311e-08 1.000000e+00
## [2,] 3.333286e-26 6.579083e-19 8.359285e-12 1.000000e+00
## [3,] 1.673301e-34 1.000000e+00 8.566423e-13 5.070375e-23
## [4,] 1.000000e+00 3.914394e-29 3.618382e-20 9.759917e-24We see that the algorithm is pretty certain tabout it’s assignments, but we might not always have this certainty for points that are somewhat “midway” between different cluster centers. For example:
## [1] 0 0 0 1Now let’s see what happens when we use a much larger bandwidth:
fit <- kernel_em(ex2$dat$y, K = 4, hmu = 50, hSigma = 50, hpi = 50, num_iter = 10, initial_fit = ex2_init_const)
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu)Let’s look at how the \(\pi\)’s and \(\mu\)’s evolve over time again:
plot_pi(fit$pi)
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu, dim = 1, show_data = FALSE)Now let’s see what happens when we use the Bayesian initialization:
fit <- kernel_em(ex2$dat$y, K = 4, hmu = 5, hSigma = 5, hpi = 5, num_iter = 10, initial_fit = ex2_init_bayes)
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu)Let’s look at how the \(\pi\)’s and \(\mu\)’s evolve over time again:
plot_pi(fit$pi)
plot_data_and_model(ex2$dat$y, fit$zest, fit$mu, dim = 1, show_data = FALSE)They look pretty similar! The algorithm is able to make up the difference between the cheap constant initialization and the improved Bayesian initialization, at least in this simple case.
3.5 Cross-Validation
We use cross validation to help with the selection of our bandwidths for the kernel smoother, implementing a 5-fold cross-validation scheme where each fold \(\mathcal{I}_1, \mathcal{I}_2, \mathcal{I}_3, \mathcal{I}_4, \mathcal{I}_5\) constitutes every 5th time point, so \(\mathcal{I}_\ell = \{\ell, \ell + 5, \ell + 10, \dots\}\).
We first fit the model on all folds apart from \(\mathcal{I}_\ell\), using \(\theta^{-\mathcal{I}_\ell}\) to denote the collection of \(\gamma_{itk}\), \(\pi_{tk}\), \(\mu_{tk}\), and \(\Sigma_{tk}\) for all \(t \in \mathcal{T} \setminus \mathcal{I}_\ell\), where \(\mathcal{T}\) is the set of all time points in our data set. We then use our prediction function \(\hat{f}_{pred}(\mathcal{I_\ell}, \theta^{-\mathcal{I}_\ell})\), which takes in all the time points \(\mathcal{I}_\ell\) at which we need predictions as well as our fit \(\theta^{-\mathcal{I}_\ell}\), and returns the parameters \(\mu_{kt},\Sigma_{kt}\), and \(\pi_{kt}\) for all time points in \(\mathcal{I}_\ell\) using the M-step equations above.
Finally, we evaluate the log-likelihood on these unseen time points \(\mathcal{I}_\ell\) using the predicted parameters from \(\hat{f}_{pred}(\mathcal{I_\ell}, \theta^{-\mathcal{I}_\ell})\), summing over all points at a given time and then averaging over all time points in \(\mathcal{I}_\ell\), to give us a single number for the fold. We then repeat this procedure for the remaining folds and take the average to give us a final cross-validation score for the current set of parameter values:
\[ \text{CV} = \frac{1}{5}\sum_{\ell=1}^{5} \frac{1}{|\mathcal{I}_\ell|} \sum_{t \in \mathcal{I}_\ell} \sum_{i \in [n_t]} \log\mathcal{L}\left(Y_{it} \mid \hat{f}_{\text{pred}}\left(\mathcal{I}_\ell, \theta^{-\mathcal{I}_\ell}\right)\right) \]
In our case, we chose to vary \(h_{\mu}\) and \(h_{\pi}\) over a grid of values, while keeping \(h_{\Sigma}\) fixed. Our grid values for \(h_{\mu}\) and \(h_{\pi}\) vary constantly on a logarithmic scale, starting at 1 and ending at the the total length of time for the data - this end point could be replaced with the first or second quartile of the total length.
For our code, we begin with a function that predicts parameter values outside the set of observed time points using the M-step equations above.
#' @param fit A list returned by `kernel_em` containing the fitted parameters (mu, Sigma, pi, and responsibilities) from the training data.
#' @param test_dates A vector of POSIXct (or POSIXt) date-time objects of length T_test representing the time points at which predictions are required.
#' @param train_dates A vector of POSIXct (or POSIXt) date-time objects of length T_train representing the time points corresponding to the training data.
#' @param train_data A list of length T_train, where each element is a matrix containing the observations for the training set at the corresponding time point.
#' @param train_biomass A list of length T_train, where each element is a numeric vector of length n_t containing the biomass (or count) for the observations in the training set.
#' @param hmu Bandwidth parameter for smoothing the mu estimates.
#' @param hSigma Bandwidth parameter for smoothing the Sigma estimates.
#' @param hpi Bandwidth parameter for smoothing the pi (mixing proportions) estimates.
#' @param scale_dates Logical flag indicating whether to rescale the date-time objects. If TRUE, the dates are converted to numeric values and rescaled (by subtracting the minimum training date and dividing by 3600); if FALSE, the dates are used directly. Defaults to TRUE.
#' @export
kernel_em_predict <- function(fit,
test_dates,
train_dates,
train_data,
train_biomass,
hmu,
hSigma,
hpi,
scale_dates = TRUE) {
num_test <- length(test_dates)
num_train <- length(train_dates)
K <- ncol(fit$pi)
d <- dim(fit$mu)[3]
mu <- array(NA, c(num_test, K, d))
Sigma <- array(NA, c(num_test, K, d, d))
pi <- matrix(NA, num_test, K)
# Convert to numeric
numeric_train_dates <- as.numeric(train_dates)
numeric_test_dates <- as.numeric(test_dates)
if (scale_dates) {
# If we are given real dates, then we do the original rescaling
min_date <- min(numeric_train_dates)
rescaled_train_dates <- (numeric_train_dates - min_date) / 3600
rescaled_test_dates <- (numeric_test_dates - min_date) / 3600
} else {
# If dates are already in hours or integer indices, treat them directly
rescaled_train_dates <- numeric_train_dates
rescaled_test_dates <- numeric_test_dates
}
# 1) Predict pi (mixing proportions) ----------------------------------------
# Weighted responsibilities (weights = biomass)
resp_weighted <- purrr::map2(train_biomass, fit$resp, ~ .y * .x)
# Sum over each mixture component across all observations
resp_sum <- purrr::map(resp_weighted, ~ colSums(.x)) %>%
unlist() %>%
matrix(ncol = K, byrow = TRUE)
# Smooth those sums across time
resp_sum_smooth <- apply(
resp_sum, 2, function(x)
stats::ksmooth(rescaled_train_dates, x, kernel = "normal", bandwidth = hpi,
x.points = rescaled_test_dates)$y
)
# Normalize to get pi
pi <- resp_sum_smooth / rowSums(resp_sum_smooth)
# 2) M-step for mu ---------------------------------------------------------
# Weighted sum of y's for each mixture component
y_sum <- purrr::map2(resp_weighted, train_data, ~ crossprod(.x, .y)) %>%
unlist() %>%
array(c(K, d, num_train)) %>%
aperm(c(3,1,2))
# Smooth each dimension across time
y_sum_smoothed <- apply(
y_sum, 2:3, function(x)
stats::ksmooth(rescaled_train_dates, x, kernel = "normal", bandwidth = hmu,
x.points = rescaled_test_dates)$y
)
# Smooth the sum of responsibilities (again, but with bandwidth hmu)
resp_sum_smooth_mu <- apply(
resp_sum, 2, function(x)
stats::ksmooth(rescaled_train_dates, x, kernel = "normal", bandwidth = hmu,
x.points = rescaled_test_dates)$y
)
# Combine smoothed sums to get mu
for (j in seq(d)) {
mu[, , j] <- y_sum_smoothed[, , j] / resp_sum_smooth_mu
}
# 3) M-step for Sigma ------------------------------------------------------
mat_sum <- array(NA, c(num_train, K, d, d))
for (tt in seq(num_train)) {
# Prepare a matrix for each observation's difference from mu
yy <- matrix(NA, nrow(train_data[[tt]]), d)
for (k_idx in seq(K)) {
for (dd in seq(d)) {
yy[, dd] <- train_data[[tt]][, dd] - fit$mu[tt, k_idx, dd]
}
mat_sum[tt, k_idx, , ] <- crossprod(yy, yy * resp_weighted[[tt]][, k_idx])
}
}
# Smooth Sigma the same way
mat_sum_smoothed <- apply(
mat_sum, 2:4, function(x)
stats::ksmooth(rescaled_train_dates, x, kernel = "normal", bandwidth = hSigma,
x.points = rescaled_test_dates)$y
)
resp_sum_smooth_Sigma <- apply(
resp_sum, 2, function(x)
stats::ksmooth(rescaled_train_dates, x, kernel = "normal", bandwidth = hSigma,
x.points = rescaled_test_dates)$y
)
for (j in seq(d)) {
for (l in seq(d)) {
Sigma[, , j, l] <- mat_sum_smoothed[, , j, l] / resp_sum_smooth_Sigma
}
}
list(mu = mu, Sigma = Sigma, pi = pi)
}We then have a function to compute the log-likelihood:
#' Compute the Average Log-Likelihood for Predicted Parameters
#'
#' This function computes the average log-likelihood of the observed data over all time points using the predicted parameters.
#'
#' @param y A list of length T, where each element is a matrix of observations at a given time point. Each matrix should have dimensions corresponding to the number of observations at that time point by the data dimension.
#' @param pred A list containing the predicted parameters from the model. It should include:
#' \describe{
#' \item{mu}{An array of predicted means with dimensions [T, K, d], where T is the number of time points, K is the number of clusters, and d is the data dimension.}
#' \item{Sigma}{An array of predicted covariance matrices with dimensions [T, K, d, d].}
#' \item{pi}{A matrix of predicted mixing proportions with dimensions [T, K].}
#' }
#'
#' @return A numeric value representing the average log-likelihood over all time points.
#' @export
compute_log_like <- function(y, pred) {
d <- ncol(y[[1]]) # Dimension of the data
ntimes <- length(y) # Number of time points
K <- dim(pred$pi)[2] # Number of clusters
log_like <- numeric(ntimes)
for (tt in seq(ntimes)) {
likelihood_tt <- 0
for (k in seq(K)) {
if (d == 1) {
# Univariate case
likelihood_k <- stats::dnorm(y[[tt]], mean = pred$mu[tt, k, 1],
sd = sqrt(pred$Sigma[tt, k, 1, 1]))
} else {
# Multivariate case
likelihood_k <- mvtnorm::dmvnorm(y[[tt]], mean = pred$mu[tt, k, ],
sigma = pred$Sigma[tt, k, , ])
}
# Weighted likelihood with mixing proportions
likelihood_tt <- likelihood_tt + pred$pi[tt, k] * likelihood_k
}
log_like[tt] <- sum(log(likelihood_tt))
}
return(mean(log_like))
}We have a small function to help ensure objects remain as matrices:
#' Ensure an Object is a Matrix
#'
#' This helper function checks whether the provided object is a matrix and, if it is not, converts it to a matrix using \code{as.matrix()}.
#'
#' @param x An object that is expected to be a matrix. If \code{x} is not already a matrix, it will be coerced into one.
#'
#' @return A matrix. If the input was not a matrix, it is converted using \code{as.matrix()}.
#'
#' @examples
#' # Example 1: x is a vector
#' vec <- c(1, 2, 3)
#' mat <- ensure_matrix(vec)
#' is.matrix(mat) # Should return TRUE
#'
#' # Example 2: x is already a matrix
#' mat2 <- matrix(1:4, nrow = 2)
#' identical(ensure_matrix(mat2), mat2) # Should return TRUE
#'
#' @export
ensure_matrix <- function(x) {
if (!is.matrix(x)) x <- as.matrix(x)
return(x)
}And now we have the function that computes the cross-validation score given a certain set of bandwidths:
#' Cross-Validated Log-Likelihood for Kernel EM Model
#'
#' This function performs K-fold cross-validation (by default, 5-fold) for selecting the bandwidth parameters in a kernel-based EM model. The data is partitioned into folds by leaving out every \code{leave_out_every}-th time point, where the \eqn{\ell}-th fold is given by
#' \deqn{\mathcal{I}_\ell = \{\ell, \ell+ \text{leave_out_every}, \ell+2 \times \text{leave_out_every}, \dots\}.}
#' For each fold, the model is fit on the remaining time points using \code{kernel_em} and predictions for the left-out points are generated using \code{kernel_em_predict}. The log-likelihood of the left-out data is computed using \code{compute_log_like}, and the final cross-validation score is the average log-likelihood over all folds.
#'
#' @param y A list of length T, where each element is a matrix of observations at a given time point.
#' @param K Number of mixture components (clusters) in the model.
#' @param dates A vector of date-time objects (e.g., of class \code{POSIXct}) of length T corresponding to the time points in \code{y}.
#' @param hmu Bandwidth parameter for smoothing the \code{mu} (mean) estimates.
#' @param hSigma Bandwidth parameter for smoothing the \code{Sigma} (covariance) estimates.
#' @param hpi Bandwidth parameter for smoothing the \code{pi} (mixing proportions) estimates.
#' @param biomass A list of length T, where each element is a numeric vector of length \eqn{n_t} containing the biomass (or count) of particles for the observations at that time point.
#' @param leave_out_every The number of folds for cross-validation (default is 5). The \eqn{\ell}-th fold is defined as the set of time points \eqn{\{\ell, \ell + \text{leave_out_every}, \ell + 2 \times \text{leave_out_every}, \dots\}}.
#' @param scale_dates Logical flag indicating whether to rescale the date-time objects. If \code{TRUE}, the dates are converted to numeric values (by subtracting the minimum date and dividing by 3600) before smoothing; if \code{FALSE}, the dates are used directly.
#'
#' @return A numeric value representing the average log-likelihood over all cross-validation folds.
#'
#' @details For each fold, the model is fit using the training data (all time points not in the current fold) and then predictions are made for the left-out time points. The log-likelihood for each fold is computed by summing the log-likelihoods over all observations and then averaging over the time points in the fold. The overall cross-validation score is obtained by averaging the log-likelihoods over all folds.
#' @export
kernel_em_cv <- function(y,
K,
dates,
hmu,
hSigma,
hpi,
biomass,
leave_out_every = 5,
scale_dates = TRUE)
{
n <- length(y)
if (leave_out_every <= 0 || leave_out_every >= n) {
stop("leave_out_every must be a positive integer smaller than the number of data points")
}
pred <- vector("list", leave_out_every)
log_like <- vector("list", leave_out_every)
for (i in seq_len(leave_out_every)) {
test_indices <- seq(i, n, by = leave_out_every)
train_data <- lapply(y[-test_indices], ensure_matrix)
train_date <- dates[-test_indices]
train_biomass <- biomass[-test_indices]
test_data <- lapply(y[test_indices], ensure_matrix)
test_date <- dates[test_indices]
test_biomass <- biomass[test_indices]
if (scale_dates){
fit_train <- kernel_em(y = train_data,
K = K,
hmu = hmu,
hSigma = hSigma,
hpi = hpi,
dates = train_date,
biomass = train_biomass)
} else {
fit_train <- kernel_em(y = train_data,
K = K,
hmu = hmu,
hSigma = hSigma,
hpi = hpi,
biomass = train_biomass)
}
pred[[i]] <- kernel_em_predict(fit = fit_train,
test_dates = test_date,
train_dates = train_date,
train_data = train_data,
train_biomass = train_biomass,
hmu = hmu,
hSigma = hSigma,
hpi = hpi,
scale_dates = scale_dates)
log_like[[i]] <- compute_log_like(test_data, pred[[i]])
}
avg_log_likelihood <- mean(unlist(log_like))
return(avg_log_likelihood)
}Finally, we have the function that performs cross validation over a grid of parameter values, where \(h_{\mu}\) and \(h_{\pi}\) vary, and \(h_{\Sigma}\) is a fixed value.
Let’s first add the packages we used to make CV run in parallel:
usethis::use_package("foreach")
usethis::use_package("doParallel")
usethis::use_package("parallel")
usethis::use_import_from("foreach", c("foreach", "%dopar%"))## ✔ Adding 'foreach' to Imports field in DESCRIPTION
## • Refer to functions with `foreach::fun()`## ✔ Adding 'doParallel' to Imports field in DESCRIPTION
## • Refer to functions with `doParallel::fun()`## ✔ Adding 'parallel' to Imports field in DESCRIPTION
## • Refer to functions with `parallel::fun()`## ✔ Adding '@importFrom foreach foreach', '@importFrom foreach %dopar%' to 'R/flowkernel-package.R'
## ✔ Writing 'NAMESPACE'#' Grid Search Cross-Validation for Kernel EM Model
#'
#' This function performs a grid search over bandwidth parameters for the kernel-based EM model via cross-validation.
#' The grid search is performed over the \code{hmu} (for the mean parameter) and \code{hpi} (for the mixing proportions)
#' while keeping \code{hSigma} fixed. Cross-validation is implemented by partitioning the data into folds by leaving out every
#' \code{leave_out_every}-th time point. For each parameter combination, the model is fit on the training data and evaluated
#' on the left-out data using the log-likelihood. The best parameters are selected as those that maximize the cross-validation score.
#'
#' @param y A list of length T, where each element is a matrix of observations at a given time point.
#' @param K Number of mixture components (clusters) in the model.
#' @param hSigma Bandwidth parameter for smoothing the \code{Sigma} (covariance) estimates.
#' @param dates A vector of date-time objects (e.g., of class \code{POSIXct}) of length T corresponding to the time points in \code{y}.
#' If \code{NULL}, the function uses the sequence of indices.
#' @param biomass A list of length T, where each element is a numeric vector of length \eqn{n_t} containing the biomass (or count)
#' for the observations at that time point. Defaults to \code{default_biomass(y)}.
#' @param leave_out_every The number of folds for cross-validation (default is 5). The \eqn{\ell}-th fold is defined as the set of
#' time points \eqn{\{\ell, \ell + \text{leave_out_every}, \ell + 2 \times \text{leave_out_every}, \dots\}}.
#' @param grid_size Number of grid points for each bandwidth parameter, resulting in a x grid. Defaults to 7
#' @param ncores Number of cores to use for parallel processing. If \code{NULL} or less than 2, the grid search is performed sequentially.
#' @param log_grid Logical flag indicating whether the grid for the bandwidth parameters should be logarithmically spaced (if \code{TRUE})
#' or linearly spaced (if \code{FALSE}). Defaults to \code{TRUE}.
#' @param grid_length_half Logical flag indicating whether to use half the total time length (or median time) for computing the end of the grid.
#'
#' @return A list containing:
#' \describe{
#' \item{results}{A data frame (converted from a matrix) of cross-validation scores, with row names corresponding to evaluated \code{hmu} values
#' and column names to evaluated \code{hpi} values.}
#' \item{best_hmu}{The best \code{hmu} value (bandwidth for smoothing \code{mu}) according to the highest CV score.}
#' \item{best_hpi}{The best \code{hpi} value (bandwidth for smoothing \code{pi}) according to the highest CV score.}
#' \item{max_cv_score}{The highest cross-validation score observed.}
#' \item{hmu_vals}{The vector of \code{hmu} values that were evaluated.}
#' \item{hpi_vals}{The vector of \code{hpi} values that were evaluated.}
#' \item{time_elapsed}{The total time elapsed (in seconds) during the grid search.}
#' }
#'
#' @details The function first determines whether the dates should be scaled based on whether \code{dates} is provided.
#' A grid of bandwidth values is then constructed (either logarithmically or linearly spaced) from the calculated range.
#' Cross-validation is performed for each parameter combination via the \code{kernel_em_cv} function. The grid search can be run
#' either sequentially or in parallel, depending on the value of \code{ncores}.
#'
#' @export
cv_grid_search <- function(y,
K,
hSigma = 10,
dates = NULL,
biomass = default_biomass(y),
leave_out_every = 5,
grid_size = 7,
ncores = NULL,
log_grid = TRUE,
grid_length_half = TRUE) {
start_time <- Sys.time()
# Decide if we are scaling dates or not
if (is.null(dates)) {
numeric_dates <- seq_along(y)
scale_dates <- FALSE
starting_date <- min(numeric_dates)
middle_date <- stats::median(numeric_dates)
if (grid_length_half) {
end_cv <- middle_date - starting_date
} else {
end_cv <- max(numeric_dates) - starting_date
}
} else {
numeric_dates <- as.numeric(dates)
scale_dates <- TRUE
starting_date <- min(numeric_dates)
middle_date <- stats::median(numeric_dates)
if (grid_length_half) {
end_cv <- (middle_date - starting_date) / 3600
} else {
end_cv <- (max(numeric_dates) - starting_date) / 3600
}
}
if (log_grid) {
# LOG-SPACED GRID
h_values <- exp(seq(log(end_cv), log(2), length = grid_size))
} else {
# LINEARLY-SPACED GRID
h_values <- seq(end_cv, 2, length.out = grid_size)
}
h_values <- round(h_values)
h_values <- unique(h_values)
h_values <- h_values[h_values > 0]
hmu_vals <- h_values
hpi_vals <- h_values
# Create a data frame of all parameter combinations
param_grid <- expand.grid(hmu = hmu_vals, hpi = hpi_vals)
# Decide whether to run in parallel or sequentially
if (is.null(ncores) || as.numeric(ncores) < 2) {
message("Running sequentially...")
# Prepare an empty data frame to store results
cv_scores <- data.frame(hmu = numeric(0), hpi = numeric(0), cv_score = numeric(0))
total <- nrow(param_grid)
for (i in seq_len(nrow(param_grid))) {
hmu <- param_grid$hmu[i]
hpi <- param_grid$hpi[i]
processed <- i
remaining <- total - i
# Print detailed progress information
message("Evaluating parameter combination ", processed, " of ", total,
": hmu = ", hmu, ", hpi = ", hpi, ". Remaining: ", remaining)
cv_score <- kernel_em_cv(
y = y,
K = K,
dates = numeric_dates,
hmu = hmu,
hSigma = hSigma,
hpi = hpi,
biomass = biomass,
leave_out_every = leave_out_every,
scale_dates = scale_dates
)
cv_scores <- rbind(cv_scores, data.frame(hmu = hmu, hpi = hpi, cv_score = cv_score))
}
} else {
message("Running in parallel on ", ncores, " cores...")
cl <- parallel::makeCluster(as.integer(ncores))
doParallel::registerDoParallel(cl)
# Export needed variables/functions
parallel::clusterExport(
cl,
varlist = c("kernel_em_cv", "ensure_matrix", "kernel_em", "kernel_em_predict",
"kernel_em_predict", "calculate_responsibilities",
"compute_log_like", "y", "K", "hSigma", "biomass",
"leave_out_every", "numeric_dates", "scale_dates"),
envir = environment()
)
# Load required packages on the workers
parallel::clusterEvalQ(cl, {
library(flowkernel)
})
cv_scores <- foreach::foreach(i = seq_len(nrow(param_grid)), .combine = rbind) %dopar% {
hmu <- param_grid$hmu[i]
hpi <- param_grid$hpi[i]
cv_score <- kernel_em_cv(
y = y,
K = K,
dates = numeric_dates,
hmu = hmu,
hSigma = hSigma,
hpi = hpi,
biomass = biomass,
leave_out_every = leave_out_every,
scale_dates = scale_dates
)
data.frame(hmu = hmu, hpi = hpi, cv_score = cv_score)
}
parallel::stopCluster(cl)
}
# Convert cv_scores to matrix form
if (nrow(cv_scores) == 0) {
stop("No cross-validation scores were computed.")
}
results <- reshape2::acast(cv_scores, hmu ~ hpi, value.var = "cv_score")
results_df <- as.data.frame(results)
# Re-label columns and rows for clarity
colnames(results_df) <- paste0("hpi_", colnames(results_df))
rownames(results_df) <- paste0("hmu_", rownames(results_df))
# Identify best hmu/hpi
max_pos <- which(results == max(results, na.rm = TRUE), arr.ind = TRUE)
best_hmu <- as.numeric(rownames(results)[max_pos[1]])
best_hpi <- as.numeric(colnames(results)[max_pos[2]])
# Timing
end_time <- Sys.time()
run_time <- as.numeric(difftime(end_time, start_time, units = "secs"))
hours <- floor(run_time / 3600)
minutes <- floor((run_time %% 3600) / 60)
seconds <- round(run_time %% 60)
cat("Best hmu:", best_hmu,
"\nBest hpi:", best_hpi,
"\nHighest CV score:", max(results, na.rm = TRUE),
"\nTime Elapsed:", run_time, "seconds =>",
hours, "hours", minutes, "minutes", seconds, "seconds\n")
results_list <- list(
results = results_df,
best_hmu = best_hmu,
best_hpi = best_hpi,
max_cv_score = max(results, na.rm = TRUE),
hmu_vals = hmu_vals,
hpi_vals = hpi_vals,
time_elapsed = run_time
)
return(results_list)
}Let us try running this on our example data, using sequential processing. To run in parallel, we would choose a value of ncores greater than 1.
ex1_cv_log_grid_results <- cv_grid_search(y = ex1$dat$y, K = 2, hSigma = 10, biomass = ex1$dat$biomass,
leave_out_every = 5, grid_size = 10, ncores = 1)## Best hmu: 3
## Best hpi: 42
## Highest CV score: -26.70831
## Time Elapsed: 131.9058 seconds => 0 hours 2 minutes 12 secondsWe can examine the cross-validation scores for each set of parameter values by calling the following:
## hpi_2 hpi_3 hpi_5 hpi_7 hpi_11 hpi_18 hpi_27
## hmu_2 -27.09489 -27.01669 -26.91560 -26.88757 -26.85268 -26.83837 -26.83041
## hmu_3 -26.98762 -26.90779 -26.80850 -26.77524 -26.75541 -26.73323 -26.72034
## hmu_5 -27.30078 -27.21382 -27.11903 -27.08647 -27.05803 -27.03449 -27.01715
## hmu_7 -28.20629 -28.12346 -28.01904 -27.99013 -27.95705 -27.93272 -27.91270
## hmu_11 -32.05725 -31.99040 -31.87798 -31.84306 -31.80663 -31.77533 -31.74727
## hmu_18 -40.23078 -40.14943 -40.05070 -40.01678 -39.97448 -39.94233 -39.92363
## hmu_27 -45.52849 -45.45158 -45.34949 -45.31565 -45.27738 -45.24562 -45.23102
## hmu_42 -46.45770 -46.37863 -46.29053 -46.26601 -46.23484 -46.22068 -46.21731
## hmu_64 -46.46337 -46.38473 -46.29238 -46.26214 -46.23645 -46.21680 -46.20546
## hmu_99 -46.45937 -46.38518 -46.28955 -46.26009 -46.23259 -46.21029 -46.20004
## hpi_42 hpi_64 hpi_99
## hmu_2 -26.81053 -26.81844 -26.92325
## hmu_3 -26.70831 -26.71402 -26.80638
## hmu_5 -27.00950 -27.03010 -27.12573
## hmu_7 -27.90229 -27.91832 -28.03440
## hmu_11 -31.73718 -31.76346 -31.87712
## hmu_18 -39.91329 -39.94013 -40.08379
## hmu_27 -45.22119 -45.22799 -45.32549
## hmu_42 -46.21370 -46.22315 -46.32529
## hmu_64 -46.20029 -46.21817 -46.31974
## hmu_99 -46.19502 -46.21597 -46.32889Note that all the scores are negative because they are log-likelihoods. The higher the score (and so the less negative), the better. Let’s add a function to plot these CV results:
#' Plot Cross-Validation Results
#'
#' This function generates an interactive 3D scatter plot of cross-validation results using Plotly.
#' It accepts a results list returned by \code{cv_grid_search} and visualizes the grid of cross-validation
#' scores along with the evaluated bandwidth values (\code{hmu} and \code{hpi}).
#'
#' @param results_list A list returned by \code{cv_grid_search}. This list should include:
#' \describe{
#' \item{results}{A data frame of cross-validation scores, where the row names correspond to evaluated \code{hmu} values and the column names to evaluated \code{hpi} values.}
#' \item{hmu_vals}{A numeric vector of the \code{hmu} bandwidth values that were evaluated.}
#' \item{hpi_vals}{A numeric vector of the \code{hpi} bandwidth values that were evaluated.}
#' }
#'
#' @return A Plotly object representing a 3D scatter plot with:
#' \describe{
#' \item{x-axis}{Evaluated \code{hmu} bandwidth values.}
#' \item{y-axis}{Evaluated \code{hpi} bandwidth values.}
#' \item{z-axis}{Corresponding cross-validation scores.}
#' }
#' @export
plot_cv_results <- function(results_list) {
# Pull out the results
results_df <- results_list$results
# Convert row/column names from strings ("hmu_99") to numeric (99)
row_nums <- as.numeric(sub("hmu_", "", rownames(results_df)))
col_nums <- as.numeric(sub("hpi_", "", colnames(results_df)))
# Sort the numeric row and column names
row_sorted <- sort(row_nums)
col_sorted <- sort(col_nums)
# Create a new, reordered matrix
# match() finds the indices of row_nums that correspond to row_sorted, etc.
row_order <- match(row_sorted, row_nums)
col_order <- match(col_sorted, col_nums)
# Reorder results_df so row i truly corresponds to row_sorted[i], etc.
results_mat <- as.matrix(results_df[row_order, col_order])
# Flatten in column-major order
cv_scores <- c(results_mat)
# Build a data frame matching the sorted bandwidths to their CV scores
df <- expand.grid(hmu = row_sorted, hpi = col_sorted)
df$cv_score <- cv_scores
# Plot in 3D
plotly::plot_ly(
data = df,
x = ~hmu,
y = ~hpi,
z = ~cv_score,
type = "scatter3d",
mode = "markers"
) %>%
plotly::layout(
title = "Cross-Validation Results",
scene = list(
xaxis = list(title = "hmu"),
yaxis = list(title = "hpi"),
zaxis = list(title = "CV Score")
)
)
}Let’s take a look at the plot:
fig <- plot_cv_results(ex1_cv_log_grid_results)
fig